Friday, April 18, 2008

Kinetic theory History
The theory for ideal gases makes the following assumptions:
In addition, if the gas is in a container, the collisions with the walls are assumed to be instantaneous and elastic.
More modern developments relax these assumptions and are based on the Boltzmann equation. These can accurately describe the properties of dense gases, because they include the volume of the molecules. The necessary assumptions are the absence of quantum effects, molecular chaos and small gradients in bulk properties. Expansions to higher orders in the density are known as virial expansions. The definitive work is the book by Chapman and Enskog but there have been many modern developments and there is an alternative approach developed by Grad based on moment expansions. In the other limit, for extremely rarefied gases, the gradients in bulk properties are not small compared to the mean free paths. This is known as the Knudsen regime and expansions can be performed in the Knudsen number.
The kinetic theory has also been extended to include inelastic collisions in granular matter by Jenkins and others.

The gas consists of very small particles, each of which has a mass.
The number of molecules is large such that statistical treatment can be applied.
These molecules are in constant, random motion. The rapidly moving particles constantly collide with each other and with the walls of the container.
The collisions of gas particles with the walls of the container holding them are perfectly elastic.
The interactions between molecules are negligible. They exert no forces on one another except during collisions.
The total volume of the individual gas molecules added up is negligible compared to the volume of the container. This is equivalent to stating that the average distance separating the gas particles is relatively large compared to their size.
The molecules are perfectly spherical in shape, and elastic in nature .
The average kinetic energy of the gas particles depends only on the temperature of the system.
Relativistic effects are negligible.
Quantum-mechanical effects are negligible. This means that the inter-particle distance is much larger than the thermal de Broglie wavelength and the molecules can be treated as classical objects.
The time during collision of molecule with the container's wall is negligible as comparable to the time between successive collisions.
The equations of motion of the molecules are time-reversible. Postulates
Pressure is explained by kinetic theory as arising from the force exerted by gas molecules impacting on the walls of the container. Consider a gas of N molecules, each of mass m, enclosed in a cuboidal container of volume V. When a gas molecule collides with the wall of the container perpendicular to the x coordinate axis and bounces off in the opposite direction with the same speed (an elastic collision), then the momentum lost by the particle and gained by the wall is:
Delta p_x = p_i - p_f = 2 m v_x,
where vx is the x-component of the initial velocity of the particle.
The particle impacts the wall once every 2l/vx time units (where l is the length of the container). Although the particle impacts a side wall once every 1l/vx time units, only the momentum change on one wall is considered so that the particle produces a momentum change on a particular wall once every 2l/vx time units.
Delta t = frac{2l}{v_x}
The force due to this particle is:
F = frac{Delta p}{Delta t} = frac{2 m v_x}{frac{2l}{v_x}} = frac{m v_x^2}{l}
The total force acting on the wall is:
F = frac{msum_j v_{jx}^2}{l}
where the summation is over all the gas molecules in the container.
The magnitude of the velocity for each particle will follow:
v^2 = v_x^2 + v_y^2 + v_z^2
Now considering the total force acting on all six walls, adding the contributions from each direction we have:
mbox{Total Force} = 2 cdot frac{m}{l}(sum_j v_{jx}^2 + sum_j v_{jy}^2 + sum_j v_{jz}^2) = 2 cdot frac{m}{l} sum_j (v_{jx}^2 + v_{jy}^2 + v_{jz}^2) = 2 cdot frac{m sum_j v_{j}^2}{l}
where the factor of two arises from now considering both walls in a given direction.
Assuming there are a large number of particles moving sufficiently randomly, the force on each of the walls will be approximately the same and now considering the force on only one wall we have:
F = frac{1}{6} left(2 cdot frac{m sum_j v_{j}^2}{l}right) = frac{m sum_j v_{j}^2}{3l}
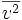The quantity frac{1}{N}sum_j v_{j}^2 can be written as overline{v^2}, where the bar denotes an average, in this case an average over all particles. This quantity is also denoted by v_{rms}^2 where vrms is the root-mean-square velocity of the collection of particles.
Thus the force can be written as:
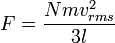
F = frac{Nmv_{rms}^2}{3l}
Pressure, which is force per unit area, of the gas can then be written as:
P = frac{F}{A} = frac{Nmv_{rms}^2}{3Al}
where A is the area of the wall of which the force exerted on is considered.
Thus, as cross-sectional area multiplied by length is equal to volume, we have the following expression for the pressure
P = {Nmv_{rms}^2 over 3V}
where V is the volume. Also, as Nm is the total mass of the gas, and mass divided by volume is density
P = {1 over 3} rho v_{rms}^2
where ρ is the density of the gas.
This result is interesting and significant, because it relates pressure, a macroscopic property, to the average (translational) kinetic energy per molecule (1/2mvrms), which is a microscopic property. Note that the product of pressure and volume is simply two thirds of the total kinetic energy.

Pressure
One can calculate the number of atomic or molecular collisions with a wall of a container per unit area per unit time.
Assuming an ideal gas, a derivation of this[1] results in an equation for total number of collisions per unit time per area:


A = frac{1}{4}frac{N}{V} v_{ave} = frac{rho}{4} sqrt{frac{8 k T}{pi m}} frac{1}{m} ,

Number of collisions with wall
The above equation tells us that the product of pressure and volume per mole is proportional to the average (translational) molecular kinetic energy. Further, the ideal gas equation tells us that this product is proportional to the absolute temperature. Putting the two together, we arrive at one important result of the kinetic theory: average molecular kinetic energy is proportional to the absolute temperature. The constant of proportionality per degree of freedom is 1/2 times Boltzmann's constant. This result is related to the equipartition theorem. Monatomic gases have 3 degrees of freedom. As noted in the article on heat capacity, diatomic gases should have 7 degrees of freedom, but the lighter gases act as if they have only 5.
Thus the kinetic energy per kelvin (monatomic ideal gas) is:
At standard temperature (273.15 K), we get:

per mole: 12.47 J
per molecule: 20.7 yJ = 129 μeV
per mole: 3406 J
per molecule: 5.65 zJ = 35.2 meV RMS speeds of molecules

Gas laws
Heat
Maxwell-Boltzmann distribution
Thermodynamics
Collision Theory
Critical temperature
Posted by at